 |
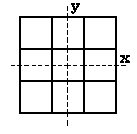
This graphic shows how the x and y axes are laid out on the last layer. |
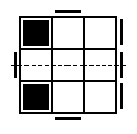 |
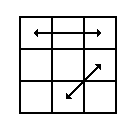
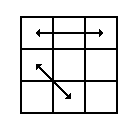
This graphic is symmetric about the x axis. |
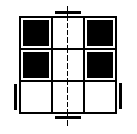 |
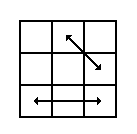
This graphic is symmetric about the y axis. |
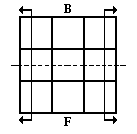 |
On the x axis reflection, the B and F faces are the only two faces that reflect off of themselves. This means that F reflects to B', F' to B, B to F', and B' to F. All other faces become their own opposites. This means R reflects to R' and so on. |
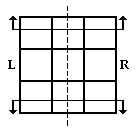 |
On the y axis reflection, the R and L faces are the only two faces that reflect off of themselves. This means that R reflects to L', R' to L, L to R', and L' to R. All other faces become their own opposites. This means U reflects to U' and so on. |